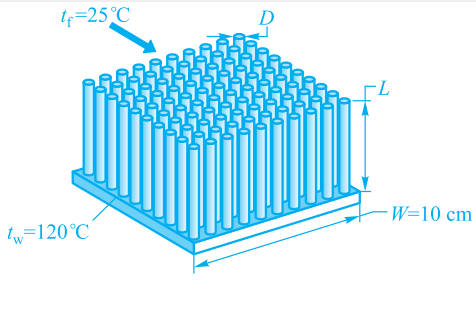
散热器的总传热面积：

\( A = W^2 + 100 \pi d L - 100 \pi {\left( \frac{d}{2} \right) ^2 } = \) m²

通道截面积：

\( A_c = WL = \) m²

根据给定入口速度 u = m/s，用关联式可以得到表面换热系数：

\( h = 5.12 u^{0.65}/d^{0.35} = \) W/(m²K)

因此由传热系数可以得到总散热量：

\[ \Phi = hA\left( T_w - T_f \right)\]

其中 T_f 为散热器中的流体平均温度。由于空气在流经散热器的过程中温度会升高，流体平均温度并不等于入口的温度，而应该使用入口和出口温度的平均值：

\[ T_f = \frac{T_{in} + T_{out}}{2}\]

同时，空气的入口温度和出口温度应该满足能量平衡：

\[ \Phi = \rho c_p u A_c \left( T_{out} - T_{in} \right) \]

如果空气的物性为常数，按照以上三个式子就可以联立求解得到总散热功率。然而，考虑到空气的密度在本题给定的温度范围内有较大变化，需要进行迭代求解。给定初始流体平均温度： T_f = (T_in + T_w)/2，然后依次进行以下步骤：
（1）用表面传热系数、传热面积、壁温和当前的流体平均温度估计总散热量；
（2）用流体平均温度查表得到空气密度：\( \rho = \rho(T_f) \)；
（3）用能量平衡式估计出口温度：

\[ T_{out} = T_{in} + \frac{\Phi }{\rho c_p u A_c} \]

（4）将流体平均温度更新为入口温度和出口温度的平均值。
由于比热容变化很小，迭代过程中将其设置为一个固定值：c_p = 1005 J/kg∙K。
次迭代后，流体平均温度基本不再变化（小于 0.001 ℃），视为求解完成。此时得到的总散热量：

\(\Phi = \) W

依次给定 0.6、1.0、1.5、2.0、2.5 m/s 的入口流速，按照上述方法计算得到散热器的散热量随空气流速而变化的曲线如下。