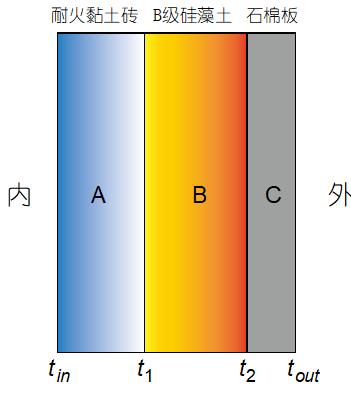
耐火黏土砖和 B 级硅藻土砖的导热系数随温度变化，其导热系数通过该层材料的平均温度确定。而温度本身是待求解的，因此需要采用迭代法。先估计各层的平均温度，确定各层材料的导热系数，然后重新计算各层材料的温度分布。经过多次计算逐步逼近得到最终结果。
具体地，首先假定各层材料均为内外层温度的平均值，然后按照以下步骤进行迭代：
（1）确定耐火黏土砖和 B 级硅藻土砖的定性温度：

\[ t_A = \frac{t_{in} - t_1}{2}\]

\[ t_B = \frac{t_1 - t_2}{2}\]

（2）计算两种材料的导热系数：

\(\lambda_A\) = 0.8 + 0.00058{t_A}_℃ W/(m∙K)
\(\lambda_B\) = 0.0477 + 0.0002{t_B}_℃ W/(m∙K)

（3）计算热流密度：

\[ q = \frac{t_{in} - t_{out}}{\frac{\delta_A}{\lambda_A} + \frac{\delta_B}{\lambda_B} + \frac{\delta_C}{\lambda_C}}\]

（4）重新计算两个材料交界面上的温度：

\[ t_1 = t_{in} + q \frac{\delta_A}{\lambda_A} \]

\[ t_2 = t_1 + q \frac{\delta_B}{\lambda_B} \]

在 次迭代后，热流密度的相对误差已低于10⁻³。计算得到耐火黏土砖和 B 级硅藻土砖的导热系数分别为：

\(\lambda_A\) = W/(m∙K)
\(\lambda_B\) = W/(m∙K)

最终得到的每平方米炉墙每小时的热损失：

\( Q = q \times 1 \times 3600\) = J

耐火黏土砖与硅藻土砖分界面上的温度：

\(t_1\) = ℃