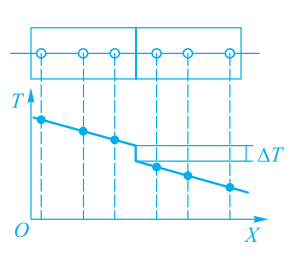
假设接触点两侧的温度均满足线性分布,左右侧的温度分布满足:
\[ T_l(x) = a_1 x + b_1 \]
\[ T_r(x) = a_2 x + b_2 \]
用测点1、2、3的位置及温度拟合接触点左侧的温度分布。采用的数据点为:(0.005, 51.2)、(0.025, 53.3)、(0.04,
54.4)。注意,题目中的长度单位mm已在数据集中转化为m。采用最小二乘法得到:
\( a_1 = \) ℃/m,\( b_1 = \) ℃
用测点4、5、6的位置及温度拟合接触点右侧的温度分布。采用的数据点为:(0.06, 56.9)、(0.075, 59.5)、(0.095, 61.6)。采用最小二乘法得到:
\( a_2 = \) ℃/m,\( b_2 = \) ℃
然后拟合得到的两个温度分布估计接触点左右两侧的温度:
\( T_{50mm}^ - = T_l(0.05) = \) ℃
\( T_{50mm}^ + = T_r(0.05) = \) ℃
因此接触点两侧温差为:
\( \Delta T = \left| T_{50mm}^+ - T_{50mm}^- \right| = \) ℃
下面计算热流密度。拟合得到的\(a_1\)、\(a_2\)即温度梯度。取两者的平均就可以估计温度梯度,进而通过给定的导热系数计算热流密度:
\( q = \lambda \left| \frac{a_1 + a_2}{2} \right| = \)
W/m2
最后由接触点两侧的温差和热流密度可以估计接触热阻:
\( R = \frac{\Delta T}{q} = \) m2K/W