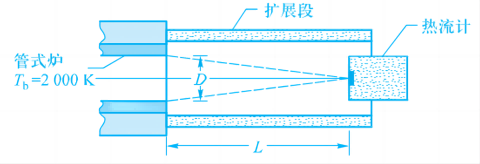
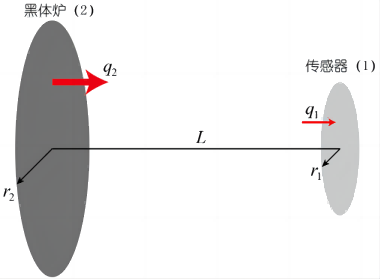
如图所示，设热流密度传感器表面为表面 1，黑体炉与附加段连接部分为表面 2。忽略附加段管壁的影响，所求的表面 1 热流密度全部来自表面 2 的辐射能贡献。


根据角系数定义，表面 2 对表面 1 的角系数 X_2,1，代表表面 2 发射的辐射能中落在表面 1 的比例。因此可表示为：

\[ X_{2,1} = \frac{\phi_{2,1}}{\phi _2} = \frac{q_1 A_1}{\sigma T_2^4 A_2}\]

根据角系数相对性原则：

\[ X_{1,2} A_1 = X_{2,1} A_2 \]

可以计算表面 1 的热流密度：

\[ q_1 = X_{1,2} \sigma T_2^4 \]

角系数 X_1,2可根据教材表 9-2 中的角系数计算式求得:

\( R_1 = r_1/L = \)

\( R_2 = r_2/L = \)

\( S = 1 + (1 + R_2^2)/R_1^2 = \)

\( X_{1,2} = \frac{1}{2} \left[ S - \left( S^2 - 4(r_2/r_1)^2 \right)^{1/2} \right] = \)

给定 T₂ = K，计算在全光谱波长下，传感器表面的热流密度为 W/m²。
给定 λ₁ = μm，λ₂ = μm。若传感器仅对该波长范围内的热辐射有接受能力，则需通过黑体辐射函数对特定波长范围的黑体辐射力进行计算：

\(\phi _2 = F_{b(\lambda_2 - \lambda _1)} E_b A_2\)

其中\( F_{b(\lambda _2 - \lambda _1)} \)为黑体辐射函数在 λ_T = ~ μm·K 的积分值：

\[ F_{b(\lambda_2 - \lambda_1)} = \int_{\lambda _1 T}^{\lambda _2 T} {\frac{c_1(\lambda T)^{-5}}{e^{c_2/(\lambda T)} - 1}\frac{1}{\sigma} \rm{d} (\lambda T)} \]

采用数值积分计算得到给定黑体温度为及波长范围下，传感器表面的热流密度为 W/m²
通过修改三个输入参数，可计算不同黑体辐射温度、不同波长范围下的传感器表面的热流密度。按照这种方法计算，得到 T_b = 2000 K ~ 3000 K 之间，全波长范围内的热流密度及上述指定波长为内的热流密度如下图所示。