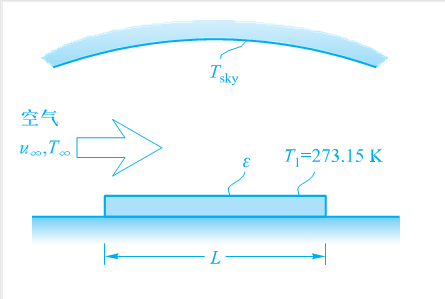
本问题的传热过程包括空气与水面之间的对流换热和水面与天空之间的辐射换热。考虑本问题的临界状态,即达到热平衡时,水面温度
Tw
恰好等于水的冰点:
Tw =
℃ =
K。
使用给定的天空温度为
Tsky = 250 K,可以按照黑体计算得到辐射换热热流密度:
\( q_r = \sigma (T_w^4 - T_{sky}^4) = \) W/m2
水面与空气能量交换为对流换热,传热达到平衡时:
\( q_c = h_{air}(T_\infty - T_w) = {q_r} = \) W/m2
其中
T∞ 为需要求解的空气的最低温度。
空气的对流换热系数
hair 与给定的流速和空气的物性相关。空气的物性受温度的影响,因此需要进行进行迭代求解。初始给定\(T_\infty^0 =
T_w\)后,然后依次进行以下步骤:
(1)根据定性温度 (
T∞ +
Tw)/2 查表获取计算所需的空气物性(包括运动粘性、导热系数和 Pr 数)。
(2)根据给定的流速和物性计算雷诺数:
\[ {\rm Re}=\frac{uL}{\nu_{air}} \]
其中:
u =
m/s,
L = 2 m,\(\nu_{air}\)
为步骤1中查表所得的运动粘性系数。
(3)根据雷诺数判断流动状态并选取对应的 Nu 公式;
层流全板长平均Nu数:
\[Nu = 0.664 {\rm Re}^{1/2} Pr^{1/3}\]
层流-湍流平均Nu数:
\[Nu = \left( 0.037{\rm Re}^{4/5} - 871 \right) Pr^{1/3} \]
其中
Pr 在步骤(1)中查表所得。
(4)根据Nu数计算对流换热系数
hair:
\[h_{air} = \frac{Nu\lambda_{air}}{L}\]
其中\(\lambda_{air}\)为步骤(1)中查表所得的运动粘性。
(5)重新计算来流空气温度:
\[ T_\infty = \frac{q_r}{h_{air}} + T_w \]
次迭代后,对流传热热流密度和辐射热流密度之间的相对偏差已小于10
−6,视为求解完成。此时得到计算得到的空气温度为:
\(T_\infty\) = ℃ = K。
来流空气低于该数值,水层就会结冰。