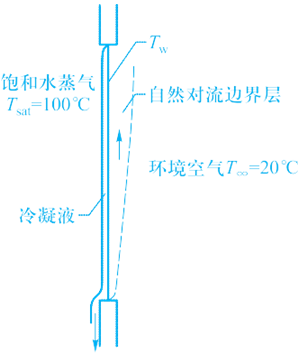
由于竖壁壁面热阻可以忽略不计，热量从饱和水蒸气到环境空气的传递过程需要经历水侧的凝结换热和空气侧的自然对流换热，根据能量平衡：

\[q = h_{air}(T_w - T_\infty ) = h_{water}(T_{sat} - T_w)\]

水侧的凝结换热采用工程修正的努塞尔理论解：

\[ h_{water} = 1.13 \left[ \frac{g \rho_l^2 \lambda_l^3 r}{\eta_l(t_{sat} - t_w)l} \right]\]

其中，g = 9.81 m/s²，\(\rho_l\) = 958.4 kg/m³，\(\lambda_l\) = 0.679 W/(m∙K)，r = \(2.257\times 10^6 \) J/kg，\(\eta_l = 2.816 \times 10^{-6}\) Pa·s，l = 0.5 m。
空气侧的换热采用均匀壁温条件的竖直壁面自然对流实验关联式：

\[ Nu_{air} = C \left( Gr \Pr \right)^n \]

其中:

\[ Gr = \frac{g \alpha_V (t_w - t_\infty)l^3}{\nu_{air}^2}    \Pr = 0.7 \]

给定环境温度\(T_\infty = \) ℃，空气的热膨胀系数 \(\alpha_V\) = 0.0034 K⁻¹。根据给定条件计算 Gr 后根据教材中的表 6-9 确定系数 C 及指数 n。最后可以计算空气侧对流换热系数：

\[ h_{air} = \frac{Nu_{air}\lambda_{air}}{l}\]

在本问题中，壁面温度需要参与两侧换热系数的计算，而且空气的部分物性随温度变化较大。因此需要采用迭代求解。
给定初始壁面温度：\(T_w = (T_{sat} + T_\infty)/2 \)，然后依次进行以下步骤：
（1）根据工程修正的努塞尔理论解，使用壁面温度预测水侧凝结换热系数。
（2）根据竖直壁面自然对流实验关联式，使用壁面温度预测空气侧的自然对流换热系数，其中的物性\(\nu_{air}\)和\(\lambda_{air}\)通过定性温度 \(T_f = (T_w + T_\infty)/2 \) 查表确定。
（3）根据能量平衡，使用两侧的传热系数更新壁面温度：

\[ T_w = \frac{h_{air}T_\infty + h_{water}T_{sat}}{h_{air} + h_{water}}\]

次迭代后，两侧热流密度的相对误差已小于 10⁻⁶，视为求解完成。此时得到计算结果为：
蒸汽向空气的传热热流密度： W/m²
每米宽度上凝结液体的流量：

\( \dot m = \frac{ql}{r} = \) kg/s

壁面温度: T_w = ℃ 水侧和空气侧的换热系数分别为：

\( h_{water} = \) W/(m²K)，\( h_{air} = \) W/(m²K)

可以看出，水侧的换热系数远大于空气侧换热系数，因此主要的热阻为空气侧的自然对流换热，热阻为：

\( R_{air} = \frac{1}{h_{air}} = \) m²K/W