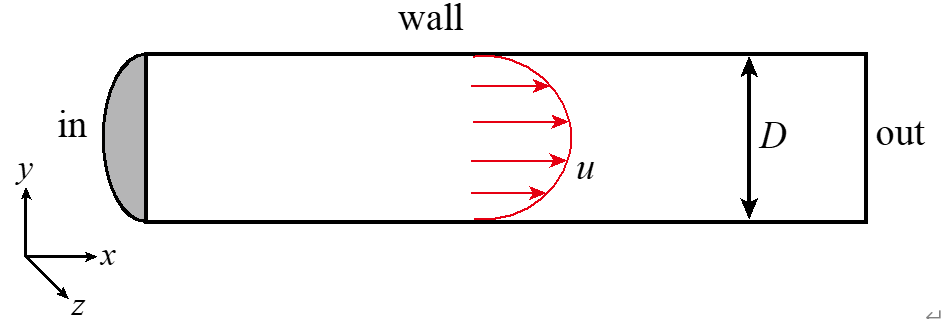
所求解的温度方程包含对流项和扩散项：

\[ \nabla \cdot \left( \rho c_p \vec u T \right) = \nabla \cdot \left( \lambda \nabla T \right) \]

在左端入口给定温度上表面设置温度 T = 0 ℃
在壁面上设置热流密度：

\( \lambda \frac{\partial T}{\partial n} = \) W/m²

在右端入口和中心截面上给定边界条件：

\[ \frac{\partial T}{\partial n} = 0 \]

采用以上的控制方程和边界条件进行计算，最终求解得到的温度场如下图所示：

可以看出，在管的前半段，管壁附近有显著的热边界层；但沿着流动方向，边界层逐渐增厚并在下游汇合与管的中心轴线。在给定热流密度的条件下，流体和管壁的温度均随着流动方向逐渐升高。从结果可以统计出流体的截面平均温度和壁面平均温度：

\[ T_b(x) = \frac{\int \limits_{A_c(x)}u_xTdA}{\int \limits_{A_c(x)}u_xdA}\]

\[ T_w(x) = \frac{\int\limits_{wall(x)} T dl }{\int\limits_{wall(x)} dl }\]

在流动方向上，流体截面平均温度和壁面平均温度变化如下图所示：
最终可以得出沿程 Nu 的变化：

\[ Nu(x) = \frac{h(x)D}{\lambda } = \frac{q_w}{T_w(x) - T_b(x)} \frac{D}{\lambda }\]

统计得到的沿程 Nu 数如下图所示：
可以看 Nu 数在出前半段较大，这是入口效应的影响，但在后半段基本不再变化，说明已经达到充分发展。对 x = 0.8 m ~ 1.0 m 范围内的 Nu 进行平均，得到给定管壁温度条件下充分发展对流换热的 Nu 数为：

\(Nu = \int_{x=0.8}^{x=1.0}{Nu(x)dx}/0.2 = \)