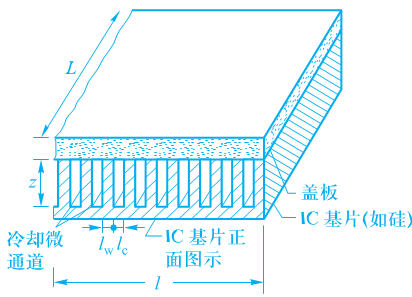
根据给定的通道宽度(
μm)和间距宽度(
μm),可以得到以下量。
单个通道的截面积:
\( A_c = W_c z = \) m2
通道数量:
\( n = \frac{W}{W_c + W_w} = \)
总传热面积:
\( A = 2n(W_c + z)L = \) m2
水力直径:
\( D_h = \frac{4W_c z}{2(W_c + z)} = \) m
通道内流速:
\( u = \frac{q_v}{nA_c} = \) m/s
下面开始计算在给定壁面温度
Tw = 23 + 71 = 94 ℃ 条件下的总传热功率。考虑水的物性在 23 ℃ ~ 94 ℃
范围内变化较大,这里采用迭代求解。
首先假定出口温度
Tout =
Tw,水的定性温度为
Tf =
(
Tin +
Tout)/2 = 58.5 ℃,然后进行以下步骤的计算:
(1)根据定性温度查表获得水的密度(\(\rho\))、粘性系数(\(\mu\))、
Pr、导热系数(\(\lambda\))、比热容(
cp)。
(2)计算雷诺数:
\[ Re = \frac{\rho u L}{\mu} \]
(3)采用齐德-泰特(Sieder-Tate)公式计算长度为L的通道的平均Nu数:
\[ Nu = 1.86\left( \frac{RePr}{L/D_h} \right)^{1/3}\left( \frac{\mu}{\mu_w} \right)^{0.14}\]
其中 \(\mu_w\) 由
Tw 查表得到。
(4)计算对流换热系数:
\[ h = \frac{Nu\lambda}{D_h}\]
(5)计算总传热功率:
\[ \Phi = hA(T_w - T_f)\]
(6)根据热平衡重新计算出口温度和定性温度:
\[T_{out} = \frac{\Phi}{q_v\rho c_p} + T_{in}\]
\[T_f = \frac{T_{in} + T_{out}}{2} \]
次迭代后,定性温度的变化量已低于 10
−3 ℃,视为求解完成。通过迭代计算得到的主要计算结果有:
Tout = ℃
Tf = ℃
Re =
Nu =
h = W/m2K
\(\Phi = \) W
估算得到 1cm × 1cm 内的总换热量为
W,如果该值大于 790 W,说明题目中的冷却效果是可以达到的。