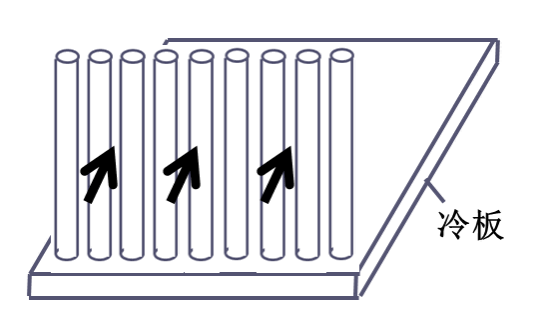
已知空气入口温度 t_in、空气入口速度 u_in、圆柱直径 d、圆柱高度 l、冷板宽度 w，假设空气出口温度 t_out，计算空气定性温度，查得空气的密度和比热容。根据热平衡迭代 3 次计算得到空气出口温度和平均温度：

\( t_{out} = \frac{\Phi}{A_{in}u_{in}\rho c_p} + t_{in} = \) ℃

\( t_f = \frac{t_{in} + t_{out}}{2} = \) ℃

式中 A_in = wl。
管束中最窄通道的平均流速：

\( u_f = \frac{u_{in}s_1}{s_1 - d} = \) m/s

由空气的定性温度查得：\(\nu_f\) = m²/s，然后计算雷诺数：

\( Re_f = \frac{u_f d}{\nu_f} = \) m/s

根据题目条件，取肋片和冷板表面的平均温度 t_w = 100 ℃，根据 t_f 和 t_w 确定 Pr_f = ，Pr_w =。
使用 Zhukauskas 的顺排管束的经验计算对流换热系数：

\[ Nu_f = 0.9 Re_f^{0.4}Pr_f^{0.36}\left( {P{r_f}/P{r_w}} \right)^{0.25},\; Re_f \in (1,10^2)\]

\[ Nu_f = 0.52 Re_f^{0.5}Pr_f^{0.36}\left( {P{r_f}/P{r_w}} \right)^{0.25},\; Re_f \in (10^2,10^3)\]

\[ Nu_f = 0.27 Re_f^{0.63}Pr_f^{0.36}\left( {P{r_f}/P{r_w}} \right)^{0.25},\; Re_f \in (10^3,2 \times 10^5)\]

\[ Nu_f = 0.033 Re_f^{0.8}Pr_f^{0.36}\left( {P{r_f}/P{r_w}} \right)^{0.25},\; Re_f \in (2 \times 10^5,2 \times 10^6)\]

得到 Nu_f = 。
根据 t_f 查表得到 \(\lambda_f\) = W/m·K，计算对流换热系数：

\(h = \frac{Nu_f \lambda_f}{d} = \) W/m²K

根据牛顿冷却公式计算所需的换热面积：

\(A = \frac{\Phi}{h(t_w - t_f)} =\) m²

上式计算出的面积包括肋片侧面积和底板未被肋片占用的面积。根据这一原则计算肋片数：

\[ N = \frac{A - w^2}{\pi dl - \pi \left( \frac{d}{2} \right)^2} \]

得到 N = ，迎风面方向有 9 根圆柱，因此需要布置 排小圆柱。