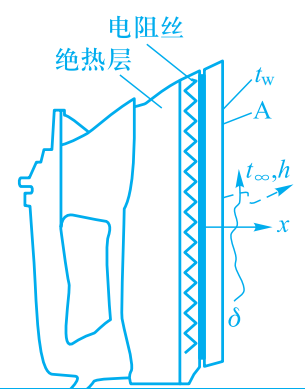
电熨斗以恒定功率发热,通过表面
A 以辐射换热和对流换热的方式将热量传递给环境。
电熨斗表面的总热流密度:
\( q = \frac{\Phi}{A} = \) W/m2
辐射换热为小平面与无限大外包空间之间的换热,辐射传热热流密度:
\[q_r = \varepsilon \sigma \left( T_w^4 - T_\infty ^4 \right)\]
电熨斗表面与环境之间的对流换热热流密度:
\[q_c = h\left( T_w - T_\infty \right)\]
根据能量平衡,\( q = q_r + q_c \),可以得到表面温度的方程:
\[\varepsilon \sigma \left( T_w^4 - T_\infty ^4 \right) + h\left( T_w - T_\infty \right) = q\]
这是一个非线性方程。可以采用线性化后用迭代方法求解:
\[ \varepsilon \sigma \left( {T_w(T_w^*)^3 - T_\infty ^4} \right) + h\left( T_w - T_\infty
\right) = q \]
其中 \(T^*\) 表示上一个迭代层次的壁面温度。给定初始壁面温度 \( T_w ^ {(0)} = T_\infty \) = 25 ℃ = 298.15 K,然后用以下式子进行迭代。
\[ T_w^{(n)} = \frac{q + h T_\infty + \varepsilon \sigma T_\infty ^4}{h + \varepsilon \sigma
(T_w^{(n-1)})^3}\]
为了提高计算的稳定性,本问题在迭代中采用了 0.5 的亚松驰因子,即:
\[ T_w^{(n)} = 0.5 \times T_w^{(n-1)} + 0.5 \times \frac{q + h T_\infty + \varepsilon \sigma
T_\infty ^4}{h + \varepsilon \sigma
(T_w^{(n-1)})^3}\]
次迭代后,热流密度的相对误差已经小于10
−6。对应所得到的壁面温度:
\({T_w} = \) K = ℃