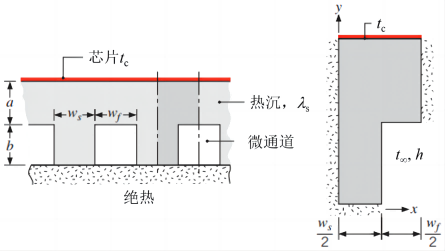
按照结构对称性,采用右图所示的单元进行数值计算,求解稳态、常物性、无内热源的导热方程:
\[ \lambda \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right)
= 0 \]
芯片表面的边界条件为:
\[ \lambda \frac{\partial T}{\partial n} = q \]
微通道表面的边界条件为:
\[ - \lambda \frac{\partial T}{\partial n} = h(T - T_f) \]
其他表面上设置绝热边界条件:
\[ \frac{\partial T}{\partial n} = 0\]
其中\(\lambda = \) 384 W/m·K 为纯铜的导热系数;
h = 30000 W/(m
2·K),
Tf = 25 ℃
为通道内流体的温度;
q =
W/m
2 为给定的芯片表面热流密度。
采用数值方法得到计算区域内的温度分布如下图。
其中最高温度为
Tmax =
℃。