平板非稳态导热过程中的温度分布

4_34.平板非稳态导热过程中的温度分布:

用数值方法计算单侧受热的无限大平板的瞬态温度场。平板厚 \(\delta\) = 0.2 m，初始温度 T₀ = 80 ℃，平板一侧被温度 \(T_\infty\) = 300 ℃ 的流体加热，另一侧绝热。设表面传热系数 h = 1163 W/(m²·K)，材料的导热系数 \(\lambda\) = 50 W/(m·K)，热扩散率 a = 1.39 × 10^-5 m²/s。
采用更小的时间步长 0.0018 s 求解，并与图 4-17 的结果作比较，讨论时间步长对求解结果及计算资源的影响。
说明：
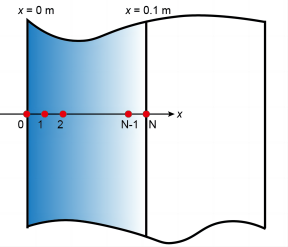
如图所示，根据对称性，选择平板左半侧作为计算区域，范围为 x = 0 ~ 0.1 m。依次选择（1）节点数量（2）时间步长后提交计算。

注意：为了防止计算振荡，应该保证网格傅里叶数小于 0.5，即：

\[ \frac{a \Delta\tau}{\Delta x^2} = \frac{a \Delta\tau}{\left( \frac{0.1}{N} \right)^2} \le \frac{1}{2}\]

要求解的一维都非稳态、常物性、无内热源的导热控制方程如下：

\[ \frac{\partial T}{\partial \tau } = a \frac{\partial^2 T}{\partial x^2} \]

左边界（x = 0 m）上满足：

\[ -\lambda \frac{\partial T}{\partial x} = h(T_\infty - T) \]

右边界（x = 0.1 m）上满足：

\[ \frac{\partial T}{\partial x} = 0 \]

对扩散项采用中心差分，对非稳态项采用向前差分，得到内部节点的显式迭代式：

\[ T_n^{(i + 1)} = \frac{a\Delta\tau}{\Delta x^2} \left( T_{n-1}^{(i)} + T_{n+1}^{(i)} - 2 T_n^{(i)} \right) + T_n^{(i)} \]

边界节点的迭代表达式根据边界条件来确定：

\[ T_0^{(i + 1)} = \frac{h T_\infty + (\lambda/\Delta x) T_1^{(i)}}{h + \lambda /\Delta x} \]

\[ T_N^{(i + 1)} = T_{N - 1}^{(i)} \]

给定节点数量，计算区域的，平均分为 N = 段

\( \Delta x = \frac{0.1}{N} = \) m

根据初始条件，给定：

\( T_n^0 = 80 \) ℃ (n = 0 ~ N)

根据已知的物性和边界条件，使用时间步长 \(\Delta \tau \) = s 进行次显式迭代计算，最终得到 1800 s（30 min）内的温度变化过程。其中，3 min、15 min 和30 min 时刻的温度分布如下图所示。

习题目录

4_34.平板非稳态导热过程中的温度分布: