习题目录
4_33.环肋肋效率计算:
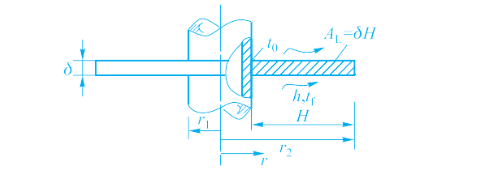
利用工具软件求解例题 4-4,并将求解结果与表 4-2, 4-3 相比较。说明: 依次输入外半径与内半径之比(r2/r1)、无量纲数 m 和节点数量,然后提交计算。
\[ m = \sqrt {\frac{h}{\lambda \delta}} (r_2 - r_1) \]
\[ \frac{1}{r} \frac{d}{dr}\left( r\frac{dT}{dr} \right) - \frac{\phi}{\lambda} = 0 \]
其中:\[ \phi = 2\frac{h(T - T_f)}{\delta} \]
引入无量纲温度及半径:\[ \Theta = \frac{T - T_f}{T_0 - T_f} R = \frac{r}{r_2 - r_1}\]
可以将导热方程转化为无量纲的形式:\[ \frac{d^2\Theta}{dR^2} + \frac{1}{R}\frac{d\Theta}{dR} - 2m^2\Theta = 0\]
边界条件为:\[ \Theta = 1 R = R_1 = \frac{r_1}{r_2 - r_1} \] \[ \frac{d\Theta}{dR} = 0 R = R_1 = \frac{r_2}{r_2 - r_1} \]
其中:\[ m = \sqrt {\frac{h}{\lambda \delta}} (r_2 - r_1) \]
并在条件中已给定 m = 。根据给定的内外半径比 r2/r1 =,可以得到无量纲长度的范围:
R1 = ,R2 =
根据给定的计算节点数量 N = ,对无量纲长度的范围进行等分,得到\(\Delta R\) = 。无量纲一维稳态导热方程的两个导数项分别用相应的中心差分格式代入,可得内部节点(n = 1 ~ N − 1)的差分方程:\[ \frac{\Theta_{n + 1} - 2\Theta_n + \Theta_{n - 1}}{\Delta R^2} + \frac{1}{R_n} \frac{\Theta _{n + 1} - \Theta _{n - 1}}{2\Delta R} - 2{m^2}{\Theta_n} = 0 \]
两个边界节点采用边界条件:\[ \Theta_0 = 1 \] \[ \Theta_{N} = \Theta_{N-1} \]
编程求解以上方程组,得到的无量纲温度分布如下图所示。\( \eta = \frac{\sum\limits_{n=1}^{N-1}{\Delta A_n \Theta _n}}{\sum\limits_{n=1}^{N-1}{\Delta A_n} } = \)
其中\(\Delta A_n = R_n \Delta R\),表示节点 n 所代表的微元体散热表面积。